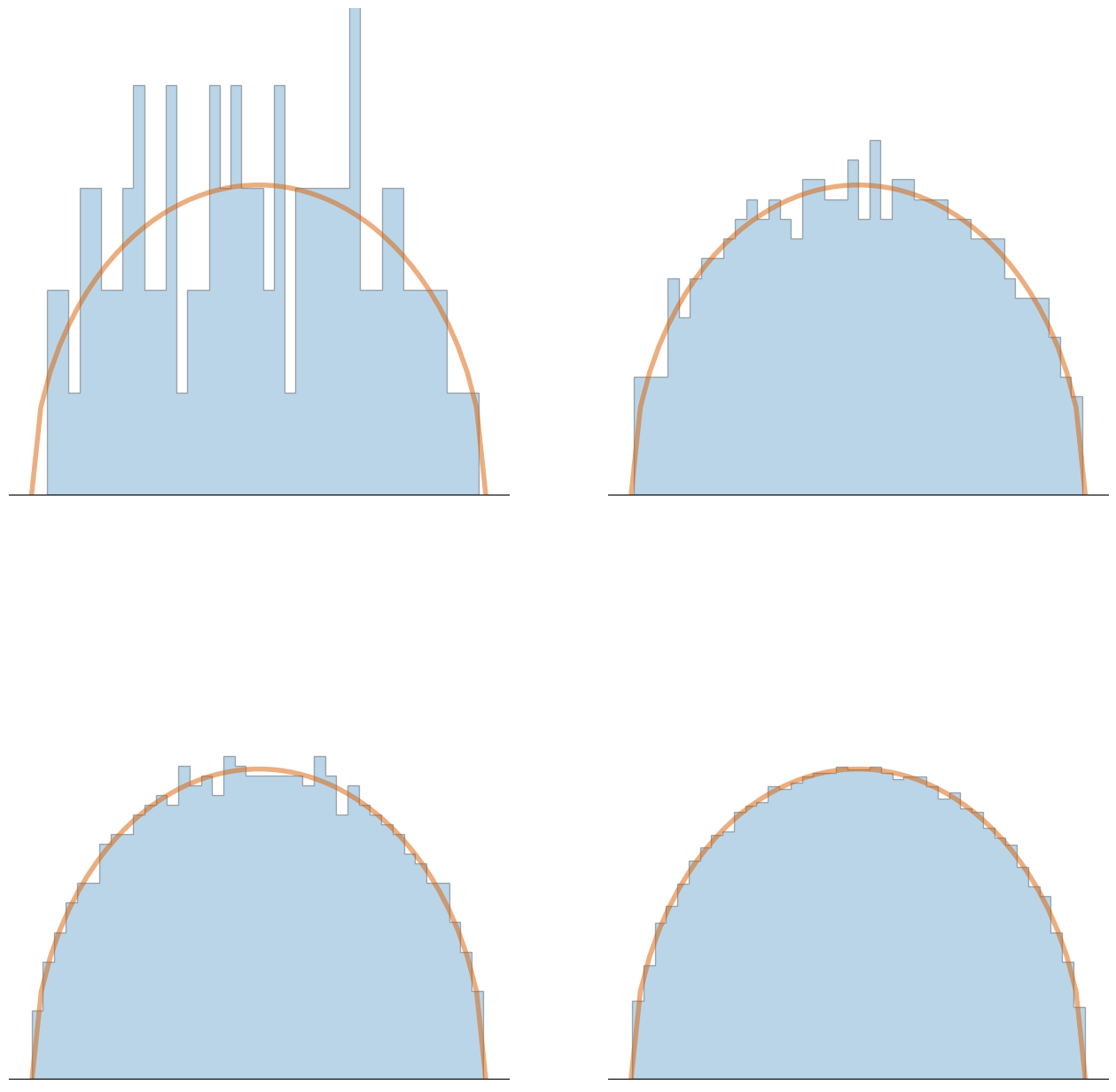
Random Matrix Theory and Machine Learning
In recent years, random matrix theory (RMT) has come to the forefront of learning theory as a tool to understand some of its most important challenges. From generalization of deep learning models to a precise analysis of optimization algorithms, RMT provides analytically tractable models.
Know more